안녕하세요. 우주신 입니다.
약 3년만에 포스팅을 하네요... 일을 하다보니 포스팅을 꾸준히 못 하고 있습니다..ㅠ
오늘은 블로그에서 가장 조회수가 높은 '[R] 상관분석...' 글을 Python으로 빠르게 변환 해봤습니다.
이번 포스팅과 다음 포스팅에서는 상관분석과 회귀분석에 대해 정리해보겠습니다.
우리는 종종 어떤 두 사건 간의 연관성을 분석해야 할 경우가 많습니다.
둘 또는 그 이상의 변수들이 서로 관련성을 가지고 변화할 때 그 관계를 분석해야 하는데,
가장 잘 알려진 방법 중 하나가 상관분석과 회귀분석 입니다.
예를 들어, GDP와 기대수명 간의 관계, 키와 몸무게 간의 관계를 보자면,
각각 두 변수 간의 선형적 관계를 상관(Correlation)이라고 하며, 이러한 관계에 대한 분석을 상관분석(correlation analysis)라고 합니다.
이번 예시에서는 당뇨와 그에 영향을 미치는 변수들 간의 관계를 분석해 보죠.
먼저 데이터는 sklearn에서 제공하는 datasets을 불러왔습니다.
import pandas as pd
import numpy as np
from sklearn import datasets
data = datsets.load_diabetes()데이터가 dictionary 형태이므로 어떤 key를 가지는지 확인해보면 아래와 같이 나오고,

여기서 data, target, feature_names 세 가지 key만 쓰겠습니다. 당연히 데이터 형태의 길이가 같은지 부터 확인해야죠.

여기서 target이 당뇨병의 수치이고 나머지 feature names에 속하는 age, sex, bmi 등등은 변수라고 보면 됩니다.
즉, 442명의 사람들을 상대로 10가지의 특성들을 나열한거죠.
우리는 bmi(체질량지수) 변수와 당뇨병의 수치(target)가 어떤 관계를 가지는지 한번 살펴봅시다.
1. 산점도 (Scatter plot)

먼저, 상관계수를 파악하기 전에 산점도를 그려 두 변수 간에 관련성을 시각적으로 파악할 수 있습니다.
X = df.bmi.values
Y = df.index.values
import matplotlib.pyplot as plt
plt.scatter(X, Y, alpha=0.5)
plt.title('TARGET ~ BMI')
plt.xlabel('BMI')
plt.ylabel('TARGET')
plt.show()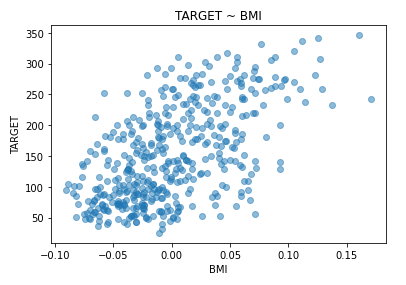
matplotlib에서 제공하는 scatter()를 통해 그린 결과 입니다.
대략 봤을 때 두 변수는 서로 양의 관계를 이루고 있는 것 같죠?
2. 공분산(Covariance) 및 상관계수(Correlation Coefficient)
산점도를 이용하면 두 변수간의 직선적인 관계를 대략적으로 파악은 가능하지만, 두 변수 사이의 관계를 어떠한 수치로 표현하지는 않아요. 그렇기에 우리는 두 변수 간의 관계를 수치로 표현하기 위해 공분산 및 상관계수를 이용합니다.
공분산은 2개의 확률변수의 상관정도를 나타내는 값인데, 만약 2 개의 변수 중 하나의 값이 상승하는 경향을 보일 때 다른 값도 상승하면 공분산의 값은 양수, 반대로 다른 값이 하강하는 경향을 보이면 공분산의 값은 음수가 나옵니다.
여러가지 방식으로 구할 수 있는데,
직접 식을 계산하면,
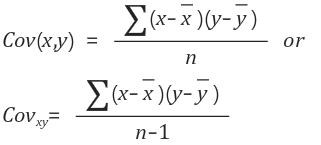
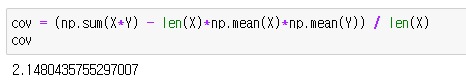
더 편하게는 numpy의 cov()를 이용하면 되죠.

두 방법 모두 비슷한 값이 나왔고 양의 값이 나온 것을 볼 수 있죠.
그러나 공분산은 상관관계의 상승 혹은 하강하는 경향을 이해할 수는 있으나 2개 변수의 측정 단위의 크기에 따라 값이 달라지므로 절대적 정도를 파악하기에는 한계가 있습니다. 즉, 2.15가 어느 정도의 양의 상관관계인지를 가늠하기가 쉽지 않죠.
그래서 공분산을 표준화 시킨 상관계수를 보다 많이 이용합니다.
상관계수는 각 변수의 표준편차를 분모로 나눠주면 되죠.

당연히, numpy는 없는게 없죠. corrcoef() 함수를 이용하면,
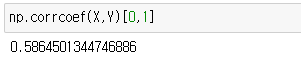
상관계수는 -1에서 1 사이의 값을 가지기에 0일 경우에는 두 변수 간의 선형관계가 전혀 없다는 것을 뜻 합니다.
보통 0.3과 0.7 사이이면, 뚜렷한 양적 선형관계로 0.7과 1.0 사이는 강한 양적 선형관계로 간주한다고 합니다.
(그러나 데이터의 특성과 샘플의 대표성 등 상황에 따라 상관계수 값 자체를 해석하는데 있어 정확한 기준은 없습니다)
위에 나온 0.58은 BMI(체질량지수)와 당뇨병수치(Target)는 뚜렷한 양적 선형관계를 이루고 있다고 볼 수 있습니다.
주의할 점은 상관계수 분석 자체가 특이 값에 민감하게 반응하기 때문에 데이터 pre-processing에 항상 주의를 기울여야 합니다.
또한 상관관계는 두 변수 간의 관련성을 의미할 뿐, 원인과 결과의 방향을 알려주지는 않습니다.
3. 상관계수의 검정
상관계수 값 자체가 유의미한가를 검정할 수도 있습니다. 그 중 하나로 p-value를 많이 이용하는데,
scipy 패키지의 stats.pearsonr()을 이용하면 상관계수와 p-value를 동시에 얻을 수 있습니다.
import scipy.stats as stats
stats.pearsonr(X,Y)
뒤 결과 값이 p-value인데, 귀무가설 "상관관계가 없다"에 대한 검정 결과 p-value가 3.46e-42라는 0에 아주 매우 가까운 값이 나왔으므로 귀무가설을 기각할 수 있음을 알 수 있습니다.
4. 그 외
그냥 궁금해서 나머지 변수들도 상관계수를 확인해 봤습니다.

당뇨병수치와 가장 상관관계가 높은 것은 bmi이고 age나 sex는 큰 관련이 없는 것으로 보이네요.
다음 시간에는 회귀분석에 대해 다뤄보겠습니다~
'Python > Basic Data Analysis' 카테고리의 다른 글
| [Python] 람다 관련 (lambda, map) (0) | 2022.04.26 |
|---|---|
| [Python] 회귀분석(Regression Analysis) [회귀식 추정, 회귀모형 검정, 적합도 파악] (2) | 2021.08.07 |
| [Python] matplotlib 이용하여 누적영역형차트, 원형차트 그리기 (0) | 2018.01.02 |
| [Python] matplotlib 이용하여 히스토그램, 산점도 그리기 (0) | 2017.12.29 |
| [Python] matplotlib 이용하여 그래프 그리기 (0) | 2017.12.29 |




댓글